昆虫の目の多くは六角形の小さなレンズ「個眼」がびっしり集まった複眼だが、どうして六角形になるのだろう。そういえばハチの巣も、六角形の穴が集まっている。こうした自然界が織りなす図形の不思議に斬り込み、2つの単純な力で幾何学的に決まる仕組みがあることが、ハエの目を使った実験で分かった。金沢大学などの研究グループが明らかにした。遺伝子が関わっていない面白さがあるという。
六角形に四角形…どうして
生活を見渡すと、お風呂のタイル、ブロック塀、ボードゲームの升目などなど、同じ形が敷き詰められたパターンはわりと四角形が目につく。これに対し生物界では、冒頭に挙げたように六角形が多いという。この理由は、六辺の長さの合計が短くしかも構造が強くなるため、低コストで丈夫に空間を埋められるという物理的安定性にあると考えられてきた。
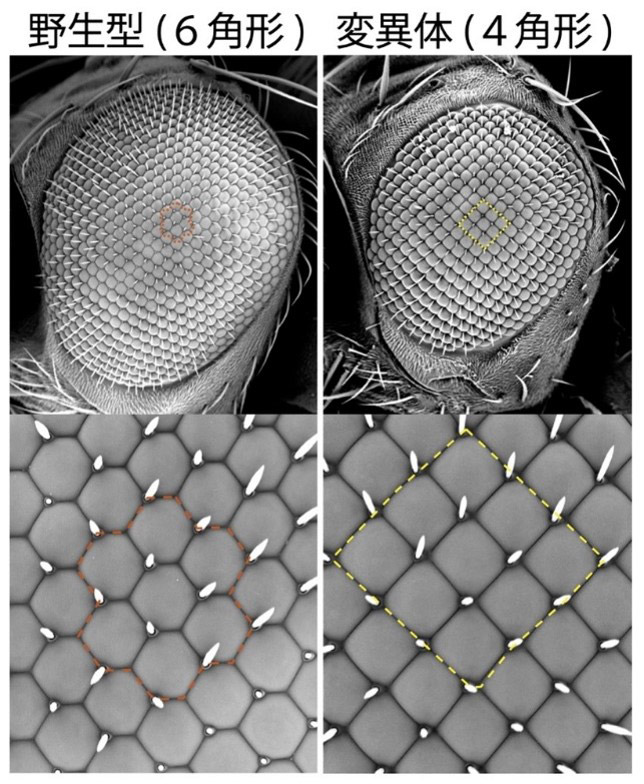
ところが、エビやロブスターの個眼は四角形で、シャコは四角形と六角形の混在なのだとか。ハエは普通は六角形だが、変異体は四角形のことがあるというから、物理的安定性だけで決まるわけではなさそうだ。ならば一体、こうした形はどんな仕組みで決まるのだろうか。
生物学と数学の融合研究を進める金沢大学新学術創成研究機構の佐藤純(まこと)教授(発生生物学、数理生物学)は「漠然と、六角形が物理法則で自然に選ばれたように信じられてきたが、(四角形のように)矛盾するケースがある。これを突き詰める研究はなく、解明したかった」という。
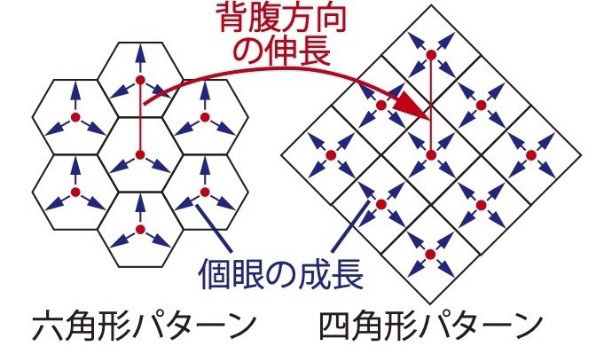
そこで佐藤教授らの研究グループは、実験動物としてよく使われるショウジョウバエの目を使い検証に挑んだ。まず、個眼が四角形の変異体は普通のハエに比べ、複眼全体の上下の幅が狭いことに着目した。この形のせいで、個眼が変形したのではないか。そう考えて変異体の目の細胞膜にレーザーを当てる実験をしたところ、複眼が上下方向に引っ張られていることが分かった。複眼の上下の幅が狭くなったために周囲から引っ張られ、それに釣られて複眼を構成する個眼も引っ張られていた。
ただ、単に引っ張られるだけだと六角形が縦長になるだけで、四角形にはなりそうにない。研究グループが物理的安定性の観点から検証の計算を実に2年にわたり続けたものの、全くうまくいかなかった。四角形ができる結論はどうしても得られなかった。
学区割りと同じ仕組み!?
手詰まり感が強まる中、研究者の1人がひらめいた。
「これ、ボロノイ分割じゃないの?」
ボロノイ分割とは、平面上の複数の点を中心に、領域を均等に分割する方法だ。というと難しく聞こえるが、公立小中学校の学区を決めるのに適した考え方だいうと、分かりやすい。どの家からも最寄りの学校に通えるように考える。すると、学校という点同士を結ぶ線分の垂直二等分線が学区の境界になる。現実の社会では行政区分や地形、学校の定員などの要因も絡むだろうが、ここではあくまで考え方の話だ。ボロノイは数学者の名前という。
ひらめきの一声を聞いた佐藤教授は当初、懐疑的だったという。「ボロノイ分割は単に定規と鉛筆で均等に分割している。何の説明にもなっていないのでは」。ところが、この考えに基づいて計算すると、個眼の形が明快に説明できてしまった。
もちろん、ハエが垂直二等分線を引いて個眼の形を決めてはいない。ただ幾何学の世界では、複数の点が風船が膨らむように同心円状に成長していき、円同士がぶつかり成長が止まって境界ができる場合にも、ボロノイ分割ができることが知られている。
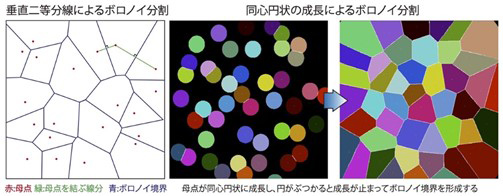

そこで、ハエのさなぎの目を成長を追って観察し、あわせてコンピューターシミュレーションを実施。その結果、実際に個眼を構成する細胞が風船のように膨らんでいき、ボロノイ分割と同様の効果を生むことを確認した。普通の六角形だけでなく変異体の四角形も、このボロノイ分割によって正確に説明できた。幾何学の世界で点が同心円状に成長するのと似たことが、個眼で起きていると考えられる。
従来の考えで単に引っ張っただけでは、縦長の六角形になる。そうではなく、引っ張る力と、風船が膨らむように押し出す力という、2つの力でボロノイ分割の形になることを突き止めた。生物の細胞や組織の形は、遺伝子の働きと物理的な制約で決まることは知られていた。これらに加え、幾何学的な分割の仕組みが存在することが明らかになった。
研究グループは金沢大学、北海道大学、富山大学、サレジオ工業高等専門学校で構成。成果は米生物学誌「カレントバイオロジー」の電子版に4月6日に掲載され、金沢大学などが同7日に発表した。研究は科学技術振興機構(JST)戦略的創造研究推進事業、文部科学省科学研究費補助金、日本学術振興会科学研究費助成事業、物質・デバイス領域共同研究拠点、武田科学振興財団、上原記念生命科学財団などの支援を受けた。
やっと解決したら…小学生でも分かる話
佐藤教授は「最近の生物学系の論文は多くが、遺伝子や分子が出てきて難解だ。ところが今回の成果では遺伝子では全くなく、単純な2つの力で説明しきれた。小学生でも理解できるだろうが、生物学者と数学者が集まってやっと解決できた。それがまた面白く、ロマンを感じた」と語る。
今回はショウジョウバエについての成果だが、この幾何学的な分割の仕組みが他の生物にもあるかもしれない。佐藤教授は具体例として、他の生物の複眼のほか、ヒマワリの花の中の種の並び方、ツクシの穂、カメやアルマジロの甲羅にみられる幾何学模様を挙げる。また、脳には多数の神経細胞が規則正しく集まった「カラム構造」がある。肝臓は細胞が多数集まった六角形の「肝小葉」で構成されているという。

これらの形は知られていても、そうなる仕組みはほとんど研究対象になってこなかった。「今回見つかった仕組みが他にも適用されるのか確かめるという、新たな研究の道筋ができた。生き物なので、同じ仕組みがあっても全然おかしくない」。
佐藤教授らは今後、複眼をさらに詳しく研究するほか、神経細胞のカラム構造も調べていくという。「何かに直接役に立つ研究ではなくても、面白さがある」。基礎科学の成果ではあるものの、将来的に人工組織や人工臓器など、生体工学関連の研究に応用される可能性もあるという。
話を聴くうち筆者はふと、以前に農園で取材したロマネスコという舶来の野菜を思い出した。ブロッコリーやカリフラワーに似ているが、芸術作品のようにも見える不思議な幾何学模様を持つ。品種改良などの人の手が加わったものもあるにせよ、数学を自然界や生き物から学んだら面白そうだ。

関連リンク
- 金沢大学などプレスリリース「複眼のタイルパターンを決定する幾何学メカニズムの解明」




