お茶の水女子大学の作道直幸(さくみち なおゆき)特任助教と奥村剛(おくむら こう)教授の研究グループは、60年以上も謎に包まれていた「速度ジャンプ」という現象の発生メカニズムを解明したと、2017年8月発表した。この成果を活用すれば、破裂しづらいゴムや、金属に代わる強度をもつプラスチックといった新素材の開発にも期待が持てるという。
複雑な現象を単純な格子モデルで捉える
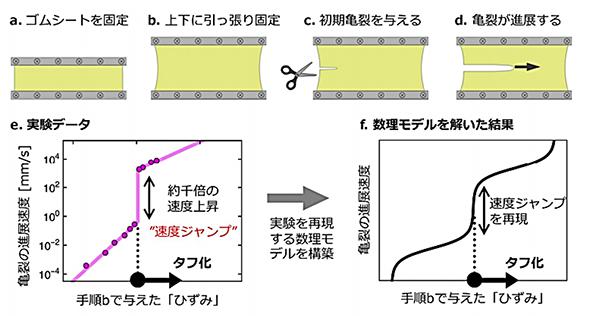
大きく膨らんだ風船に針を刺すと、大きな音を立てて一瞬で破裂する。これは「速度ジャンプ」という現象が発生した結果だ。速度ジャンプとは、ゴムに生じた亀裂の進む速度が、秒速1ミリメートル未満の低速から、秒速1メートル以上の高速へと急激に変わる現象をいう(図1-e)。“膨らませた風船に貼ったセロハンテープの上から針を刺すと風船は破裂しない”、そんなマジックを子どもの頃に体験した方も多いと思うが、タネを明かせば、これはセロハンテープが速度ジャンプの発生を抑止することでできるマジックなのだ。
速度ジャンプという現象が知られるようになったのは今から60年以上前。しかし、その発生メカニズムは長い間、謎のままだった。ゴムは非線形粘弾性体※1という複雑な挙動を示す物体で、そのゴムに起きる速度ジャンプも複雑なメカニズムで起きていると考えられていた。今回、研究グループは本質を損なうことなく、現象を大胆に単純化することで、この謎の解明を阻む壁を突破した。
※1 力を加えると変形するが、力を除くと元に戻る物体を「弾性体」と呼ぶ。その中で「フックの法則」(力を加えたときの物体の変形の度合いが、加えた力に比例することを示す法則)に従うような物体を「線形弾性体」、従わない物体を「非線形弾性体」という。「非線形粘弾性体」はさらに粘性ももつ。
速度ジャンプの現象を単純化し、数式で表すために、研究グループが採った方法は格子モデルの活用だった。格子モデルとは、対象を格子状に区切って、その格子点の値で対象の状態を簡潔に表現するモデルをいう。状態が単純化され、数値が扱いやすくなるため、数値シミュレーションや解析などでよく使われる。本研究においては、まず、ゴムシートを格子状に並んだ質点(大きさはないが重さのある点)として捉えて格子モデルに表した(図2-a)。次に、亀裂がどのように進展するのかに注目。亀裂をかたどる質点と、亀裂の先端が伸びていく先の質点のみを解析対象とした(図2-b)。さらに、ゴムの持つ粘性(ねばねばした性質)・弾性(ばねのような性質)という性質に関する標準的な理論(線形粘弾性理論)を考慮して数理モデルを構築することで、実験結果を再現し得るひとつの数式を導くことに成功した(図1-f)。
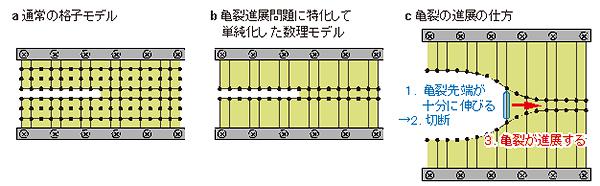
本研究の最大のポイントは、格子モデルで亀裂の問題を扱うときに、本質的で決して取り去ることができない亀裂直上の格子点だけを考えることにしたことだった。これまでも多くの研究者が格子モデルを用いてこの課題に取り組んできたが、今回、本質だけを見極めてフォーカスすることで、亀裂という数学的に取り扱いの難しい問題が格段に取り扱いやすくなり、ブレークスルーにつながった。
ゴムの「ガラス化」が速度ジャンプを引き起こす
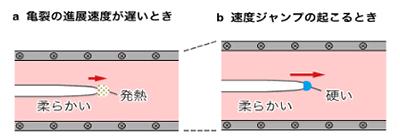
そもそもゴムは、引っ張るスピードにより3種類の性質をもつことが知られてきた。ゆっくり引っ張ると、私たちが日常で使うようなしなやかな伸び縮み方をし、少し速く引っ張ると発熱を伴う。さらに速く引っ張ると「ガラス化」し、硬くて脆い固体のようになる。
今回、構築した数理モデルを研究グループが厳密に解いた結果、亀裂の進展速度が低速(秒速1ミリメートル未満)のときは、速度が徐々に上がり、また先端を発熱させながら亀裂が進み(図3-a)、進展速度が限界値を超えると先端でガラス化して速度ジャンプが起き、一気に裂けることを突き止めた(図3-b)。ゴムがもつ3種類の性質を念頭におけば、ごく自然にイメージできるシナリオではあるが、従来、これを説明できる数理モデルは存在せず、今回構築した数理モデルで、世界で初めて科学的な裏づけのあるメカニズムの解明に至った。
また今回構築した数理モデルを厳密に解いた解は、三次方程式を含む相当複雑な形をしていたが、この解を数値的に評価してみることで、速度ジャンプが確かに存在していることが分かったそうだ。さらに、試行錯誤を重ねてその解を詳細に調べた結果、ガラス化の現象による速度ジャンプが存在することを数学的に証明でき、より完成度の高い研究に仕上がったという。
ゴムの破裂がガラス化に起因するならば、逆に考えれば、ガラス化しない、あるいはガラス化に耐えられる素材になれば、速度ジャンプは起こらず、破裂したり急にちぎれたりしない新しいゴムになる可能性がある。また、ゴムは原子が鎖のように長く連なった「高分子」が、化学反応により網目のようになった構造をしている。プラスチックやスライムも同様の構造をしていることから、これらの物質でもゴムと同様のメカニズムで速度ジャンプが生じているかもしれない。
ガラス化を抑えるためのメカニズムも解明
次に研究チームは、どのような策を講じれば速度ジャンプを抑制できるかの考察を進めた。そして、速度ジャンプが発生する瞬間の破壊表面エネルギー(破壊に必要なエネルギー)を抑制するための物理的パラメータを用いて、シンプルに表す数式を導き出した(図4)。この数式は、網目の大きさやガラス化したときの先端の硬さ、ゴムが切れるときのひずみの大きさからなる。この式の値が大きくなるほど、速度ジャンプは起こりにくくなる(タフになる)。網目構造を粗くすることとガラス化したときの硬さを強化することが、耐久性や耐摩耗性がより向上した丈夫なゴムの開発に役立つことが、この数式から判明した。
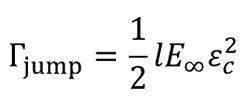
「現実的・日常的」な問題にも物理学を
今後、研究グループでは、本研究成果を理論的に発展させて、ゴム以外の高分子材料に広く適用できないかを検討していくという。また、シート状の物質に着目して、ゴム以外のさまざまな高分子材料で亀裂進展の実験を進め、今回とは別タイプのシンプルな式の発見も目指しているそうだ。
このように、新たな可能性やアイデアを試し確かめていくことで、将来的にはこれまでにないタフな新素材が開発されることが期待される。例えば、自動車のタイヤに使うゴムを十分な耐久性を保持したまま薄くすることができれば、重量軽減による燃費の向上や、生産時の消費エネルギーや原材料の低減などが期待できる。プラスチックがタフ化されて金属の代用ができるようになれば、自動車や飛行機のボディを軽量化できるだろう。タフな素材の開発によって私たちの暮らしにも大きな変化が訪れるかもしれない。
基礎研究は応用研究に比べて注目されることが少ないが、科学全体の礎となり、知の領域を広げていく。本研究も、そんな基礎研究のひとつだ。私たちの未来の生活をがらりと変えてしまうかもしれないこの研究の“次の一手”に注目していきたい。
(サイエンスライター 橋本 裕美子)




